Concrete Example#

%load_ext autoreload
%autoreload 2
%matplotlib inline

Imports#

from fastai.vision.all import *
from aiking.data.external import * #We need to import this after fastai modules
import pandas as pd
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import mutual_info_regression

Getting Dataset#

# kaggle datasets download -d sinamhd9/concrete-comprehensive-strength
path = untar_data("kaggle_datasets::sinamhd9/concrete-comprehensive-strength"); path

Path('/content/drive/MyDrive/PPV/S_Personal_Study/aiking/data/concrete-comprehensive-strength')

path.ls()

(#1) [Path('/content/drive/MyDrive/PPV/S_Personal_Study/aiking/data/concrete-comprehensive-strength/Concrete_Data.xls')]

df = pd.read_excel(path/'Concrete_Data.xls'); df.head()

	Cement (component 1)(kg in a m^3 mixture)	Blast Furnace Slag (component 2)(kg in a m^3 mixture)	Water (component 4)(kg in a m^3 mixture)	Superplasticizer (component 5)(kg in a m^3 mixture)	Coarse Aggregate (component 6)(kg in a m^3 mixture)	Fine Aggregate (component 7)(kg in a m^3 mixture)	Age (day)	Concrete compressive strength(MPa, megapascals)
0	540.0	0.0	162.0	2.5	1040.0	676.0	28	79.986111
1	540.0	0.0	162.0	2.5	1055.0	676.0	28	61.887366
2	332.5	142.5	228.0	0.0	932.0	594.0	270	40.269535
3	332.5	142.5	228.0	0.0	932.0	594.0	365	41.052780
4	198.6	132.4	192.0	0.0	978.4	825.5	360	44.296075

df.columns

Index(['Cement (component 1)(kg in a m^3 mixture)',
       'Blast Furnace Slag (component 2)(kg in a m^3 mixture)',
       'Fly Ash (component 3)(kg in a m^3 mixture)',
       'Water  (component 4)(kg in a m^3 mixture)',
       'Superplasticizer (component 5)(kg in a m^3 mixture)',
       'Coarse Aggregate  (component 6)(kg in a m^3 mixture)',
       'Fine Aggregate (component 7)(kg in a m^3 mixture)', 'Age (day)',
       'Concrete compressive strength(MPa, megapascals) '],
      dtype='object')

X = df.copy()
y = X.pop('Concrete compressive strength(MPa, megapascals) ')
X

	Cement (component 1)(kg in a m^3 mixture)	Blast Furnace Slag (component 2)(kg in a m^3 mixture)	Fly Ash (component 3)(kg in a m^3 mixture)	Water (component 4)(kg in a m^3 mixture)	Superplasticizer (component 5)(kg in a m^3 mixture)	Coarse Aggregate (component 6)(kg in a m^3 mixture)	Fine Aggregate (component 7)(kg in a m^3 mixture)	Age (day)
0	540.0	0.0	0.0	162.0	2.5	1040.0	676.0	28
1	540.0	0.0	0.0	162.0	2.5	1055.0	676.0	28
2	332.5	142.5	0.0	228.0	0.0	932.0	594.0	270
3	332.5	142.5	0.0	228.0	0.0	932.0	594.0	365
4	198.6	132.4	0.0	192.0	0.0	978.4	825.5	360
...	...	...	...	...	...	...	...	...
1025	276.4	116.0	90.3	179.6	8.9	870.1	768.3	28
1026	322.2	0.0	115.6	196.0	10.4	817.9	813.4	28
1027	148.5	139.4	108.6	192.7	6.1	892.4	780.0	28
1028	159.1	186.7	0.0	175.6	11.3	989.6	788.9	28
1029	260.9	100.5	78.3	200.6	8.6	864.5	761.5	28

1030 rows × 8 columns

     79.986111
     61.887366
     40.269535
     41.052780
     44.296075
          ...    
  44.284354
  31.178794
  23.696601
  32.768036
  32.401235
Name: Concrete compressive strength(MPa, megapascals) , Length: 1030, dtype: float64

df.describe().T

	count	mean	std	min	25%	50%	75%	max
Cement (component 1)(kg in a m^3 mixture)	1030.0	281.165631	104.507142	102.000000	192.375000	272.900000	350.000000	540.000000
Blast Furnace Slag (component 2)(kg in a m^3 mixture)	1030.0	73.895485	86.279104	0.000000	0.000000	22.000000	142.950000	359.400000
Fly Ash (component 3)(kg in a m^3 mixture)	1030.0	54.187136	63.996469	0.000000	0.000000	0.000000	118.270000	200.100000
Water (component 4)(kg in a m^3 mixture)	1030.0	181.566359	21.355567	121.750000	164.900000	185.000000	192.000000	247.000000
Superplasticizer (component 5)(kg in a m^3 mixture)	1030.0	6.203112	5.973492	0.000000	0.000000	6.350000	10.160000	32.200000
Coarse Aggregate (component 6)(kg in a m^3 mixture)	1030.0	972.918592	77.753818	801.000000	932.000000	968.000000	1029.400000	1145.000000
Fine Aggregate (component 7)(kg in a m^3 mixture)	1030.0	773.578883	80.175427	594.000000	730.950000	779.510000	824.000000	992.600000
Age (day)	1030.0	45.662136	63.169912	1.000000	7.000000	28.000000	56.000000	365.000000
Concrete compressive strength(MPa, megapascals)	1030.0	35.817836	16.705679	2.331808	23.707115	34.442774	46.136287	82.599225

def get_mi_scores(X, y, discrete_features=None):
    mi_scores = None
    if discrete_features:
        mi_scores = mutual_info_regression(X, y, discrete_features=discrete_features)
    else:
        mi_scores = mutual_info_regression(X, y)
    mi_scores = pd.Series(mi_scores, name="MI Scores", index=X.columns).sort_values(ascending=False)
    return mi_scores

get_mi_scores(X,y)

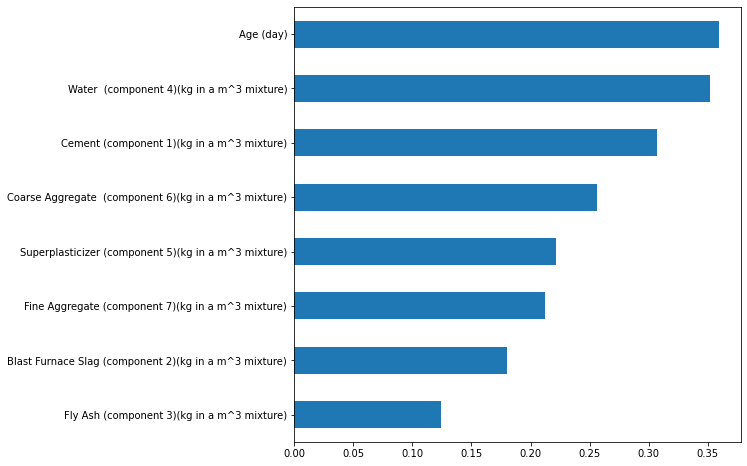
Age (day)                                                0.365659
Water  (component 4)(kg in a m^3 mixture)                0.357788
Cement (component 1)(kg in a m^3 mixture)                0.306730
Coarse Aggregate  (component 6)(kg in a m^3 mixture)     0.254809
Superplasticizer (component 5)(kg in a m^3 mixture)      0.222348
Fine Aggregate (component 7)(kg in a m^3 mixture)        0.210143
Blast Furnace Slag (component 2)(kg in a m^3 mixture)    0.180440
Fly Ash (component 3)(kg in a m^3 mixture)               0.121087
Name: MI Scores, dtype: float64

mi_scores = get_mi_scores(X,y)
mi_scores.sort_values(ascending=True).plot(kind='barh', figsize=(8,8))

<matplotlib.axes._subplots.AxesSubplot at 0x7f3547391450>

Baseline Model#

baseline = RandomForestRegressor(criterion='absolute_error', random_state=0)
baseline

RandomForestRegressor(criterion='absolute_error', random_state=0)

doc(cross_val_score)

`cross_val_score`[source]

cross_val_score(estimator, X, y=None, groups=None, scoring=None, cv=None, n_jobs=None, verbose=0, fit_params=None, pre_dispatch=`'2n_jobs'*, **error_score**=*nan`*)

Evaluate a score by cross-validation.

Read more in the :ref:User Guide <cross_validation>.

Parameters¶

estimator : estimator object implementing 'fit' The object to use to fit the data.

X : array-like of shape (n_samples, n_features) The data to fit. Can be for example a list, or an array.

y : array-like of shape (n_samples,) or (n_samples, n_outputs), default=None The target variable to try to predict in the case of supervised learning.

groups : array-like of shape (n_samples,), default=None Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a "Group" :term:cv instance (e.g., :class:GroupKFold).

scoring : str or callable, default=None A str (see model evaluation documentation) or a scorer callable object / function with signature scorer(estimator, X, y) which should return only a single value.

Similar to :func:`cross_validate`
but only a single metric is permitted.

If `None`, the estimator's default scorer (if available) is used.

cv : int, cross-validation generator or an iterable, default=None Determines the cross-validation splitting strategy. Possible inputs for cv are:

- `None`, to use the default 5-fold cross validation,
- int, to specify the number of folds in a `(Stratified)KFold`,
- :term:`CV splitter`,
- An iterable that generates (train, test) splits as arrays of indices.

For `int`/`None` inputs, if the estimator is a classifier and `y` is
either binary or multiclass, :class:`StratifiedKFold` is used. In all
other cases, :class:`KFold` is used. These splitters are instantiated
with `shuffle=False` so the splits will be the same across calls.

Refer :ref:`User Guide <cross_validation>` for the various
cross-validation strategies that can be used here.

.. versionchanged:: 0.22
    `cv` default value if `None` changed from 3-fold to 5-fold.

n_jobs : int, default=None Number of jobs to run in parallel. Training the estimator and computing the score are parallelized over the cross-validation splits. None means 1 unless in a :obj:joblib.parallel_backend context. -1 means using all processors. See :term:Glossary <n_jobs> for more details.

verbose : int, default=0 The verbosity level.

fit_params : dict, default=None Parameters to pass to the fit method of the estimator.

pre_dispatch : int or str, default='2*n_jobs' Controls the number of jobs that get dispatched during parallel execution. Reducing this number can be useful to avoid an explosion of memory consumption when more jobs get dispatched than CPUs can process. This parameter can be:

    - ``None``, in which case all the jobs are immediately
      created and spawned. Use this for lightweight and
      fast-running jobs, to avoid delays due to on-demand
      spawning of the jobs

    - An int, giving the exact number of total jobs that are
      spawned

    - A str, giving an expression as a function of n_jobs,
      as in '2*n_jobs'

error_score : 'raise' or numeric, default=np.nan Value to assign to the score if an error occurs in estimator fitting. If set to 'raise', the error is raised. If a numeric value is given, FitFailedWarning is raised.

.. versionadded:: 0.20

Returns¶

scores : ndarray of float of shape=(len(list(cv)),) Array of scores of the estimator for each run of the cross validation.

Examples¶

from sklearn import datasets, linear_model from sklearn.model_selection import cross_val_score diabetes = datasets.load_diabetes() X = diabetes.data[:150] y = diabetes.target[:150] lasso = linear_model.Lasso() print(cross_val_score(lasso, X, y, cv=3)) [0.33150734 0.08022311 0.03531764]

	Type	Default
`estimator`
`X`
`y`	`NoneType`	`None`
`groups`	`NoneType`	`None`
`scoring`	`NoneType`	`None`
`cv`	`NoneType`	`None`
`n_jobs`	`NoneType`	`None`
`verbose`	`int`	`0`
`fit_params`	`NoneType`	`None`
`pre_dispatch`	`str`	`2*n_jobs`
`error_score`	`float`	`nan`

Synthetic Ratio Features#

X2 = X.copy()
X2['FCRatio'] = X['Fine Aggregate (component 7)(kg in a m^3 mixture)']/X['Coarse Aggregate  (component 6)(kg in a m^3 mixture)']
X2['AggCmtRatio'] = (X['Fine Aggregate (component 7)(kg in a m^3 mixture)']+\
                    X['Coarse Aggregate  (component 6)(kg in a m^3 mixture)'])/X['Cement (component 1)(kg in a m^3 mixture)']
X2['WtrCmtRatio'] = X['Water  (component 4)(kg in a m^3 mixture)']/X['Cement (component 1)(kg in a m^3 mixture)']
X2

	Cement (component 1)(kg in a m^3 mixture)	Blast Furnace Slag (component 2)(kg in a m^3 mixture)	Fly Ash (component 3)(kg in a m^3 mixture)	Water (component 4)(kg in a m^3 mixture)	Superplasticizer (component 5)(kg in a m^3 mixture)	Coarse Aggregate (component 6)(kg in a m^3 mixture)	Fine Aggregate (component 7)(kg in a m^3 mixture)	Age (day)	FCRatio	AggCmtRatio	WtrCmtRatio
0	540.0	0.0	0.0	162.0	2.5	1040.0	676.0	28	0.650000	3.177778	0.300000
1	540.0	0.0	0.0	162.0	2.5	1055.0	676.0	28	0.640758	3.205556	0.300000
2	332.5	142.5	0.0	228.0	0.0	932.0	594.0	270	0.637339	4.589474	0.685714
3	332.5	142.5	0.0	228.0	0.0	932.0	594.0	365	0.637339	4.589474	0.685714
4	198.6	132.4	0.0	192.0	0.0	978.4	825.5	360	0.843724	9.083082	0.966767
...	...	...	...	...	...	...	...	...	...	...	...
1025	276.4	116.0	90.3	179.6	8.9	870.1	768.3	28	0.883002	5.927641	0.649783
1026	322.2	0.0	115.6	196.0	10.4	817.9	813.4	28	0.994498	5.063004	0.608318
1027	148.5	139.4	108.6	192.7	6.1	892.4	780.0	28	0.874048	11.261953	1.297643
1028	159.1	186.7	0.0	175.6	11.3	989.6	788.9	28	0.797191	11.178504	1.103708
1029	260.9	100.5	78.3	200.6	8.6	864.5	761.5	28	0.880856	6.232273	0.768877

1030 rows × 11 columns

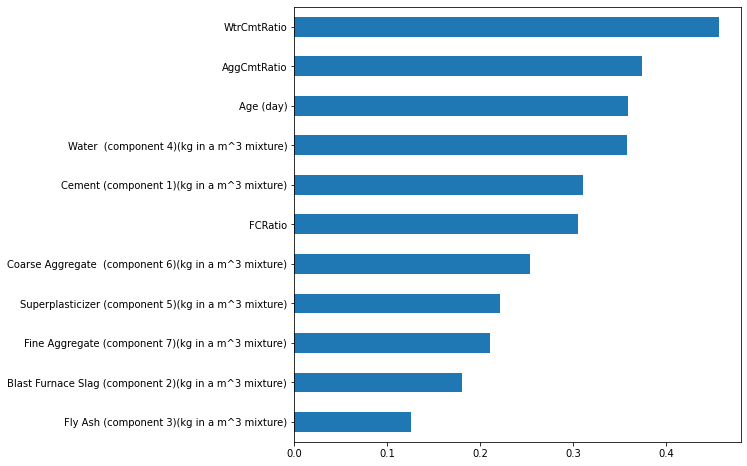
mi_scores = get_mi_scores(X2,y)
mi_scores.sort_values(ascending=True).plot(kind='barh', figsize=(8,8))

<matplotlib.axes._subplots.AxesSubplot at 0x7f354716f190>

model = RandomForestRegressor(criterion='absolute_error', random_state=0)
model

RandomForestRegressor(criterion='absolute_error', random_state=0)

model_score = cross_val_score(baseline, X2, y, cv=5, scoring="neg_mean_absolute_error"); model_score

array([ -7.81818502,  -6.81671063,  -6.07947033,  -4.21662952,
       -15.11848874])

model_score = -1 * model_score.mean()
print(f"MAE Baseline Score: {model_score:.4}")

MAE Baseline Score: 8.01

model_score*100/y.mean() # Percentage error against mean

22.36287219555449

Mutual Information#

First step in feature engineering -> Create a feature utility metric to evaluate association between feature and target
Example of this metric -> Mutual Information
Mutual Information ref: Kaggle Feature Engineering
- Relationships between two quantities
- Difference from correlation: MI can detect any kind of relationship whereas Correlation only detects linear relationships
MI esp. useful at start of Feature Engineering
- Easy to use and interpret
- Computationally efficient
- Theoretically well founded
- Resistant to overfitting
- Can detect any kinds of relationships
MI measures relationship in terms of uncertainty( or entropy)
- Extent to which knowledge of one quantity reduces uncertainty about the other
- If you know the variable, How much more confident you would be about the target?
- Relative Potential of feature
- Univariate metric -> Can’t detect interaction
- Theoretically, between 0 to inf. In practice rarely above 2.0
- Actual usefulness depends on the model you use it in. Sometime you need to transform the data to make the association evident to model which it can then learn

AIBook

Concrete Example

Contents

Concrete Example#

Imports#

Getting Dataset#

Baseline Model#

`cross_val_score`[source]

Parameters¶

Returns¶

Examples¶

See Also¶

Synthetic Ratio Features#

Mutual Information#

AIBook

Concrete Example

Contents

Concrete Example#

Imports#

Getting Dataset#

Baseline Model#

cross_val_score[source]

Parameters¶

Returns¶

Examples¶

See Also¶

Synthetic Ratio Features#

Mutual Information#

`cross_val_score`[source]