Understanding Effect Size from Differences in Mean#

Synopsis#

  • Working Definition : Working from a sample of a population and trying to estimate something about the world

  • We are trying to generalize from what we measure about the world from a sample.

  • Statistical Inference

    • Estimate Effect Size

    • Quantify precision of the result[ Confidence Interval / standard error]

    • Doing Hypothesis testing: [What is chance that the difference is zero? Or in another words, it happened by chance?]

Imports#

import numpy as np
import scipy as sp
import scipy.stats as stats
import matplotlib as plt
import matplotlib.pyplot as plt
from ipywidgets import interact, interactive, fixed
import ipywidgets as widgets
from
# seed the random number generator so we all get the same results
np.random.seed(17)

# some nice colors from http://colorbrewer2.org/
COLOR1 = '#7fc97f'
COLOR2 = '#beaed4'
COLOR3 = '#fdc086'
COLOR4 = '#ffff99'
COLOR5 = '#386cb0'

%matplotlib inline

Part 1#

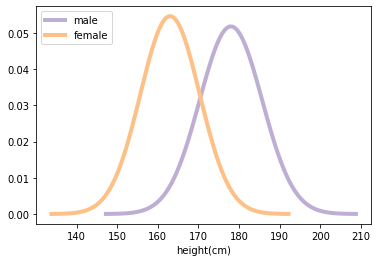
Population distribution#

mu1, sig1 = 178, 7.7
male_height = stats.norm(mu1, sig1); male_height

<scipy.stats._distn_infrastructure.rv_frozen at 0x7f18e0daac70>

mu2, sig2 = 163, 7.3
female_height = stats.norm(mu2, sig2); female_height

<scipy.stats._distn_infrastructure.rv_frozen at 0x7f1819eb5730>

Function to evaluate normal(Gaussian) PDF#

def eval_pdf(rv, n=4):
    mean, std = rv.mean(), rv.std()
    xs = np.linspace(mean - n*std, mean + n*std, 100)
    ys = rv.pdf(xs)
    return xs, ys

xs_male, ys_male = eval_pdf(male_height)
xs_female, ys_female = eval_pdf(female_height)

fig= plt.figure()
ax = fig.gca()
ax.plot(xs_male, ys_male, label='male', linewidth=4, color=COLOR2)
ax.plot(xs_female, ys_female, label='female', linewidth=4, color=COLOR3)
plt.xlabel('height(cm)')
plt.legend(loc='upper left')
plt.show()
../../_images/01_effect_size_13_0.png

Random Sampling from distribution/population#

male_sample = male_height.rvs(1000); male_sample.shape

(1000,)

female_sample = female_height.rvs(1000); female_sample.shape

(1000,)

Mean of sample will be close to population but not exactly same

mean1, std1 = male_sample.mean(), male_sample.std()
mean1, std1

(178.16511665818112, 7.84199617128995)

mean2, std2 = female_sample.mean(), female_sample.std()
mean2, std2

(163.48610226651135, 7.382384919896662)

difference_in_mean = mean1-mean2
difference_in_mean

14.679014391669767

relative_difference_by_sample = (2*difference_in_mean/(mean1+mean2))*100
relative_difference_by_sample

8.59298230392402

relative_difference_by_distribution = (2*difference_in_mean/(mu1+mu2))*100
relative_difference_by_distribution

8.609392605084908

relative_difference_by_male = difference_in_mean/mu1*100
relative_difference_by_male

8.24663729869088

relative_difference_by_female = difference_in_mean/mu2*100
relative_difference_by_female

9.005530301637894

Which one is correct?

  • Here things are symmetric so you can express in either way

  • What about taking avg?

  • There may be situation where you have a treatment group and control group. There you might want to do

\(Diff_{treatment}/ mean_{control}\)

Part 2#

Understanding the overlap, threshold, misclassification rate#

Alternative way to quantify difference is to see how much they overlap

Simple threshold#

simple_thresh = (mean1 + mean2)/2; simple_thresh

170.82560946234622

Threshold(more appropriate)#

thresh = (mean1*std2+mean2*std1)/(std1+std2); thresh

170.6040359174722

Overlap#

How many male below threshold ?

male_below_thresh = sum(male_sample<thresh); male_below_thresh

164

How many female above threshold ?

female_above_thresh = sum(female_sample>thresh); female_above_thresh

174

The “overlap” is the area under the curves that ends up on the wrong side of the threshold

male_overlap = male_below_thresh / len(male_sample)
female_overlap = female_above_thresh / len(female_sample)
male_overlap, female_overlap

# overlap = (male_overlap + female_overlap)

(0.164, 0.174)

Misclassification Rate#

misclassification_rate = (male_overlap+female_overlap)/2; misclassification_rate

0.16899999999999998

Probability of superiority#

Another way to quantify the difference between distributions is what’s called “probability of superiority”, which is a problematic term.

  • In this context it’s the probability that a randomly-chosen man is taller than a randomly-chosen woman.

sum(male_sample > female_sample), (male_sample> female_sample).mean()

(918, 0.918)
Distribution of Superiority#
male_sample[:5]

array([178.44105417, 170.49028233, 170.94885314, 188.07981499,
       171.51692076])

np.random.shuffle(male_sample)
male_sample[:5]

array([180.02059072, 185.18602683, 177.45366243, 176.95014285,
       186.13226315])

s = []
for i in range(100):
    np.random.shuffle(male_sample)
    np.random.shuffle(female_sample)
    s.append((male_sample> female_sample).mean())

prob_sup_sample = np.array(s)

plt.hist(prob_sup_sample)
plt.show()
../../_images/01_effect_size_50_0.png 
@interact
def plot_prob_sup(n_trials=(100, 1000), n_bins=(20, 40)):
    s = []
    for i in range(n_trials):
        np.random.shuffle(male_sample)
        np.random.shuffle(female_sample)
        s.append((male_sample> female_sample).mean())
    prob_sup_sample = np.array(s)
    mean = np.mean(prob_sup_sample)
    std = np.std(prob_sup_sample)
    plt.title(f"$\mu$ {mean:0.01f} \n $\sigma$ {std:0.03f} \n n {n_trials}")
    
    plt.hist(prob_sup_sample, bins=n_bins, color=COLOR1)
    plt.axvline(x=mean, color=COLOR3)
    plt.axvline(x=mean-2*std, color=COLOR2)
    plt.axvline(x=mean+2*std, color=COLOR2)
    plt.xlim(.890, .950)
    plt.xlabel("N[male_height > female_height]")
    plt.show()

Note

Overlap(or misclassification rate) & “probability of superiority” have 2 good properties:

  • As probabilities, they don’t depend on UOM- Comparable between studies

  • Expressed in Operational terms ( sense of what practical effect the difference makes)

Cohens’ Effect Size#

Difference in mean , standardized by dividing by std. dev

\(d = \frac{\bar{x_1} - \bar{x_2}}{s}\)

Pooled standard deviation

\(s = \sqrt{\frac{n_1{s_1}^2+n_2{s_2}^2}{n_1+n_2}}\)

Implementation cohen’s effectsize#
def cohen_effectsize(grp1, grp2):
    diff = grp1.mean() - grp2.mean()
    
    n1, n2 = len(grp1), len(grp2)
    var1 = grp1.var()
    var2 = grp2.var()
    
    pooled_var = (n1*var1+n2*var2)/(n1+n2)
    
    d = diff/np.sqrt(pooled_var)
    return d

cohen_effectsize(male_sample, female_sample)

1.9274780043619493
Implementation overlap_superiority#
def overlap_superiority(control, treatment, n=1000):
    
    control_sample = control.rvs(n)
    treatment_sample = treatment.rvs(n)
#     mean1, std1 = control_sample.mean(), control_sample.std()
#     mean2, std2 = treatment_sample.mean(), control_sample.std()
# #     treatment_sample.mean()
#     thresh = (mean1*std2+mean2*std1)/(std1+std2)
    thresh = (control.mean()+treatment.mean())/2
    
    control_above = sum(control_sample > thresh)
    treatment_below = sum(treatment_sample < thresh)
    overlap = (control_above + treatment_below)/n
    superiority =  (treatment_sample> control_sample).mean()
    return overlap , superiority
    

overlap_superiority(male_height, female_height)

(1.672, 0.083)

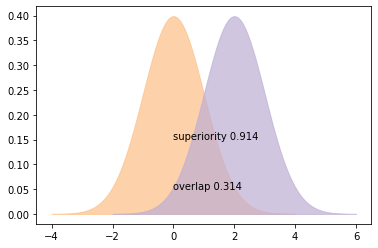
def plot_pdfs(cohen_d=2):
    control = stats.norm(0,1)
    treatment = stats.norm(cohen_d,1)
    xs, ys = eval_pdf(control)
    plt.fill_between(xs, ys, label='control', 
                        color=COLOR3, alpha=0.7)
    xs, ys = eval_pdf(treatment)
    plt.fill_between(xs, ys, label='treatment', 
                        color=COLOR2, alpha=0.7)
    o, s = overlap_superiority(control, treatment)
    plt.text(0, 0.05, 'overlap ' + str(o))
    plt.text(0, 0.15, 'superiority ' + str(s))
    plt.show()
    

plot_pdfs(2)
../../_images/01_effect_size_61_0.png 
slider = widgets.FloatSlider(min=0, max=4.1, value=2)
interactive(plot_pdfs, cohen_d=slider)

Note

  • Cohen effect size non dimensional

  • Can be used to calculate overlap and probability of superiority