Recurrent Neural Networks for Language Model
Contents
Recurrent Neural Networks for Language Model#
Imports#
from trax.fastmath import numpy as np
import random
import trax
2022-07-29 06:27:08.825369: W tensorflow/stream_executor/platform/default/dso_loader.cc:64] Could not load dynamic library 'libcudart.so.11.0'; dlerror: libcudart.so.11.0: cannot open shared object file: No such file or directory
RNN Calculation Viz#
w_hh = np.full((3,2), 1); w_hh, w_hh.shape
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)
(DeviceArray([[1, 1],
[1, 1],
[1, 1]], dtype=int32, weak_type=True),
(3, 2))
w_hx = np.full((3,3), 9); w_hx, w_hx.shape
(DeviceArray([[9, 9, 9],
[9, 9, 9],
[9, 9, 9]], dtype=int32, weak_type=True),
(3, 3))
w_h1 = np.concatenate((w_hh, w_hx), axis=1); w_h1, w_h1.shape
(DeviceArray([[1, 1, 9, 9, 9],
[1, 1, 9, 9, 9],
[1, 1, 9, 9, 9]], dtype=int32, weak_type=True),
(3, 5))
w_h2 = np.hstack((w_hh, w_hx)); w_h2, w_h2.shape
(DeviceArray([[1, 1, 9, 9, 9],
[1, 1, 9, 9, 9],
[1, 1, 9, 9, 9]], dtype=int32, weak_type=True),
(3, 5))
h_t_prev = np.full((2,1),1); h_t_prev, h_t_prev.shape
(DeviceArray([[1],
[1]], dtype=int32, weak_type=True),
(2, 1))
x_t = np.full((3,1), 9); x_t, x_t.shape
(DeviceArray([[9],
[9],
[9]], dtype=int32, weak_type=True),
(3, 1))
ax_1 = np.concatenate((h_t_prev, x_t), axis=0); ax_1
DeviceArray([[1],
[1],
[9],
[9],
[9]], dtype=int32, weak_type=True)
ax_2 = np.vstack((h_t_prev, x_t)); ax_2,ax_2.shape
(DeviceArray([[1],
[1],
[9],
[9],
[9]], dtype=int32, weak_type=True),
(5, 1))
w_h1@ax_1
DeviceArray([[245],
[245],
[245]], dtype=int32, weak_type=True)
w_hh@h_t_prev + w_hx@x_t
DeviceArray([[245],
[245],
[245]], dtype=int32, weak_type=True)
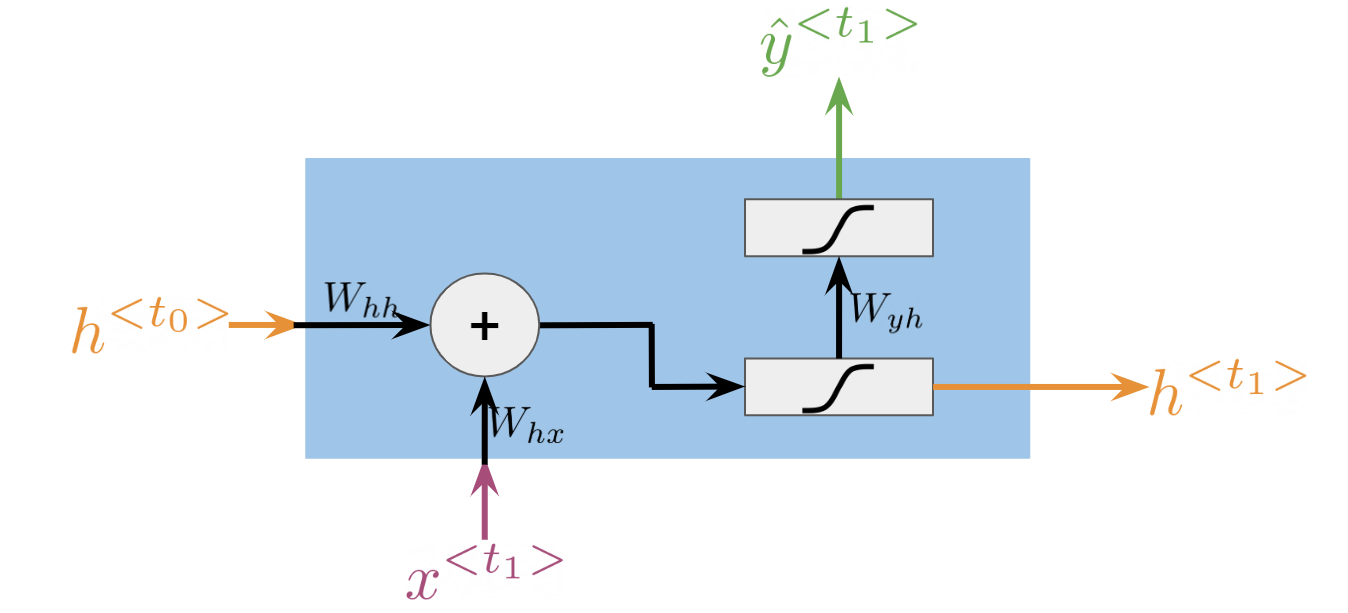
Vanilla RNNs, GRUs and the scan function#
RNN
(6)#
(7)#
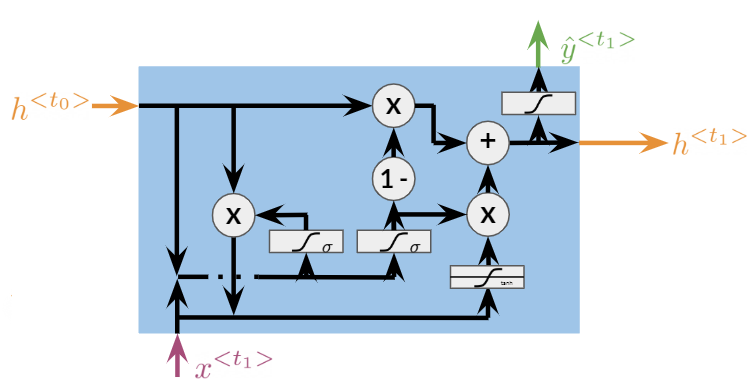
GRU
(8)#
(9)#
(10)#
(11)#
def sigmoid(x):
return 1.0/(1.0+np.exp(-x))
def forward_VRNN(inputs, weights):
x_t, h_t_prev = inputs
stack = np.vstack([h_t_prev, x_t])
w_h, _, _,w_y, b_h, _,_,b_y = weights
h_t = sigmoid(w_h@stack + b_h)
# print(h_t.shape)
y_t = sigmoid(w_y@h_t+b_y)
return y_t, h_t
def forward_GRU(inputs, weights):
x_t, h_t_prev = inputs
stack = np.vstack([h_t_prev, x_t])
w_r, w_u, w_h,w_y, b_r, b_u,b_h,b_y = weights
T_r = sigmoid(w_r@stack + b_r)
T_u = sigmoid(w_u@stack + b_u)
c_t = np.tanh(w_h@np.vstack((T_r*h_t_prev, x_t)) + b_h)
h_t = T_u*c_t+(1-T_u)*h_t_prev
y_t = sigmoid(w_y@h_t+b_y)
return y_t, h_t
def scan(fn, elems, weights, h_0=None):
h_t = h_0
ys = []
for x in elems:
y, h_t = fn([x, h_t], weights)
ys.append(y)
return np.array(ys), h_t
random.seed(10)
emb = 128
T = 256 # Number of variables in sequence
h_dim = 16 # Hidden state dimensions
h_0 = np.zeros((h_dim, 1));h_0.shape
random_key = trax.fastmath.random.get_prng(seed=0)
w1 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, emb+h_dim)); w1
w2 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, emb+h_dim)); w2
w3 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, emb+h_dim)); w3
w4 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, h_dim)); w4
b1 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, 1)); b1
b2 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, 1)); b2
b3 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, 1)); b3
b4 = trax.fastmath.random.normal(key = random_key,
shape = (h_dim, 1)); b4
X = trax.fastmath.random.normal(key = random_key,
shape = (T, emb, 1)); X
weights = [w1, w2, w3, w4, b1, b2, b3, b4]; weights
w1.shape, h_0.shape, X.shape, X[0].shape
((16, 144), (16, 1), (256, 128, 1), (128, 1))
inputs = X[0], h_0
weights = weights
forward_VRNN(inputs, weights)
forward_GRU(inputs, weights)
(DeviceArray([[0.98875064],
[0.90948516],
[0.83860266],
[0.605238 ],
[0.8174015 ],
[0.8074013 ],
[0.9864478 ],
[0.19836329],
[0.23806544],
[0.03616815],
[0.9230415 ],
[0.897435 ],
[0.81876415],
[0.06574202],
[0.14956403],
[0.820773 ]], dtype=float32),
DeviceArray([[ 9.9999964e-01],
[ 1.0000000e+00],
[ 9.9392438e-01],
[-1.2257343e-04],
[-7.2951213e-02],
[-2.5626263e-02],
[-2.4690714e-09],
[-2.0006059e-01],
[ 7.9664338e-01],
[-4.0450820e-07],
[-1.1183748e-03],
[-1.2833535e-09],
[-7.8878832e-09],
[ 9.9999976e-01],
[ 9.5781153e-01],
[-7.0657270e-06]], dtype=float32))
np.array([1,2,3])*np.array([2,2,2])
DeviceArray([2, 4, 6], dtype=int32)
%time scan(fn=forward_VRNN, elems=X, weights=weights, h_0=h_0)
CPU times: user 2.12 s, sys: 43.6 ms, total: 2.17 s
Wall time: 2.16 s
(DeviceArray([[[0.9844214 ],
[0.86315817],
[0.808999 ],
...,
[0.05173129],
[0.21562287],
[0.7522172 ]],
[[0.9830031 ],
[0.8508622 ],
[0.7086585 ],
...,
[0.02949953],
[0.27303317],
[0.9107685 ]],
[[0.5616716 ],
[0.42216417],
[0.02124172],
...,
[0.49089074],
[0.6445939 ],
[0.0898608 ]],
...,
[[0.96719635],
[0.3858212 ],
[0.06641304],
...,
[0.89807695],
[0.8543829 ],
[0.7933321 ]],
[[0.9930194 ],
[0.75615996],
[0.3213525 ],
...,
[0.46565428],
[0.5535333 ],
[0.7318801 ]],
[[0.81508607],
[0.3935613 ],
[0.07889035],
...,
[0.2907602 ],
[0.2841384 ],
[0.30343485]]], dtype=float32),
DeviceArray([[9.9991798e-01],
[9.7653759e-01],
[2.6515589e-05],
[8.7920368e-01],
[1.0000000e+00],
[9.4612682e-01],
[9.9921525e-01],
[1.0000000e+00],
[1.0000000e+00],
[1.1614484e-02],
[9.9999189e-01],
[9.9806911e-01],
[2.3502709e-02],
[1.6757324e-08],
[8.7104484e-09],
[2.2113952e-10]], dtype=float32))
%time scan(fn=forward_GRU, elems=X, weights=weights, h_0=h_0)
CPU times: user 386 ms, sys: 0 ns, total: 386 ms
Wall time: 384 ms
(DeviceArray([[[0.98875064],
[0.90948516],
[0.83860266],
...,
[0.06574202],
[0.14956403],
[0.820773 ]],
[[0.99207675],
[0.8274236 ],
[0.7019363 ],
...,
[0.08724681],
[0.2603313 ],
[0.9303203 ]],
[[0.96868426],
[0.65789413],
[0.04706543],
...,
[0.02912108],
[0.76775664],
[0.1878842 ]],
...,
[[0.99862254],
[0.68557423],
[0.68682545],
...,
[0.01584747],
[0.6382734 ],
[0.27868038]],
[[0.9979925 ],
[0.67977065],
[0.7547641 ],
...,
[0.01567412],
[0.54346865],
[0.24606723]],
[[0.9998665 ],
[0.38725543],
[0.9630767 ],
...,
[0.00373541],
[0.6321914 ],
[0.9655915 ]]], dtype=float32),
DeviceArray([[ 0.99998415],
[ 0.99973965],
[ 0.93683696],
[-0.44143844],
[ 1. ],
[ 0.99857235],
[ 0.99990374],
[ 1. ],
[ 1. ],
[ 0.85161185],
[ 0.99997693],
[ 0.9956449 ],
[ 0.37345803],
[ 0.99998754],
[ 0.98146665],
[ 0.9999966 ]], dtype=float32))
Perplexity Calculations#
The perplexity is a metric that measures how well a probability model predicts a sample and it is commonly used to evaluate language models. It is defined as:
As an implementation hack, you would usually take the log of that formula (so the computation is less prone to underflow problems)
After taking the logarithm of


