EuroCoinProblem

Import

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import seaborn as sns
import empiricaldist
from empiricaldist import Pmf, Distribution
from ipywidgets import interact, interactive, fixed

euro = Pmf.from_seq(range(101))

euro

	probs
0	0.009901
1	0.009901
2	0.009901
3	0.009901
4	0.009901
...	...
96	0.009901
97	0.009901
98	0.009901
99	0.009901
100	0.009901

101 rows × 1 columns

Custom Likelihood

def likelihood_euro(data, hypo):
#     print(data, hypo)
    x = hypo/100
    # outcome = data
    if data == 'H':
        return x
    else:
        return 1-x

euro = Pmf.from_seq(range(101))
euro.update(likelihood_euro, 'H')
euro.plot()

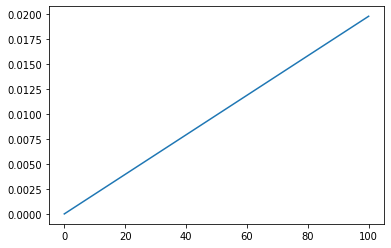
euro.update(likelihood_euro, 'H')
euro.plot()

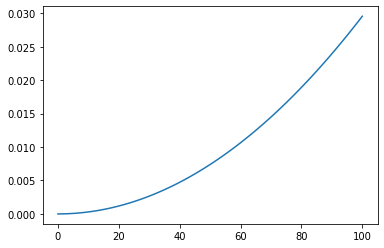
euro.update(likelihood_euro, 'T')
euro.plot()

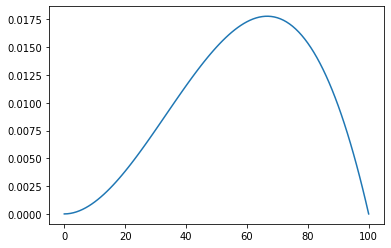
euro.update(likelihood_euro, 'H')
euro.plot()

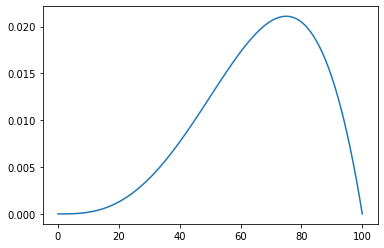
outcome = 'HHHHHHTTT'
euro = Pmf.from_seq(range(101))
for data in outcome:
    euro.update(likelihood_euro, data)
    
euro.plot()

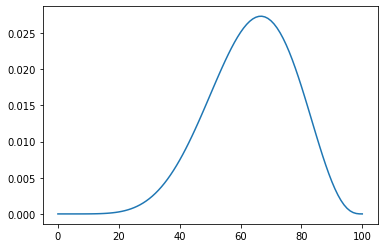
outcome = 'H'*140+'T'*110
euro = Pmf.from_seq(range(101))
for data in outcome:
    euro.update(likelihood_euro, data)
    
euro.plot()

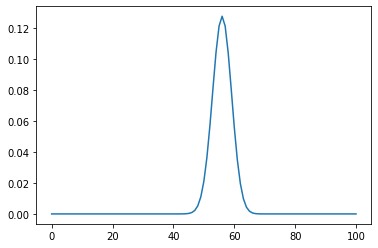
euro.mean()

55.95238095238095

np.percentile(euro, [10,90])

array([1.62410199e-96, 3.48751559e-02])

#MAP - Maximum aposteori probability
euro.max_prob()

56

euro.quantile(0.5)

array(56.)

euro.credible_interval(0.9)

array([51., 61.])

Note

Assuming prior and credible is true

euro.mean??

np.sum(euro.ps*euro.qs)

55.95238095238095

euro.max_prob??

euro.idxmax()

56

euro.credible_interval??

Effect of Different Priors

def TriangularPrior():
    """Makes a Suite with a triangular prior
    """
    
    suite = Pmf(name='triangle')
    for x in range(0,51):
        suite[x] = x
    for x in range(51, 101):
        suite[x] = 100-x
    suite.normalize()
    return suite

euro1 = Pmf.from_seq(range(101), name='uniform')
euro1.plot()

euro2 = TriangularPrior()
euro2.plot()

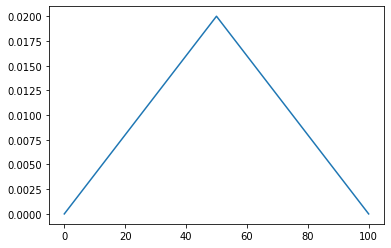
def decorate_euro(title):
    """Labels the axes.
    
    title: string
    """
    plt.xlabel('Probability of heads')
    plt.ylabel('PMF')
    plt.title(title)

euro1 = Pmf.from_seq(range(101), name='uniform prior')
euro1.plot(color='steelblue')
euro2 = TriangularPrior()
euro2.plot(color='red', label='triangular prior')

plt.legend()
decorate_euro("Prior Distribution")

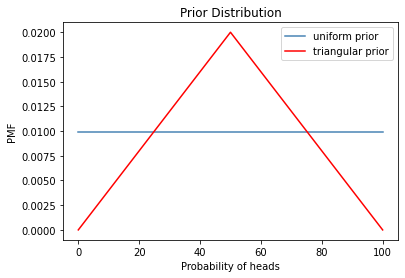
outcome = 'H'*140+'T'*110

euro1 = Pmf.from_seq(range(101), name='uniform')
euro1.plot()
euro2 = TriangularPrior()
euro2.plot()

for data in outcome:
    euro1.update(likelihood_euro, data)
    euro2.update(likelihood_euro, data)
euro1.plot()
euro2.plot()
plt.legend()
decorate_euro("Posterior Distribution")

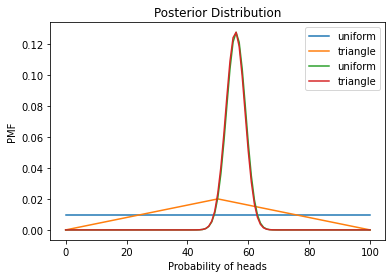
outcome = 'H'*14+'T'*11

euro1 = Pmf.from_seq(range(101), name='uniform')
euro1.plot()
euro2 = TriangularPrior()
euro2.plot()

for data in outcome:
    euro1.update(likelihood_euro, data)
    euro2.update(likelihood_euro, data)
euro1.plot()
euro2.plot()
plt.legend()
decorate_euro("Posterior Distribution")

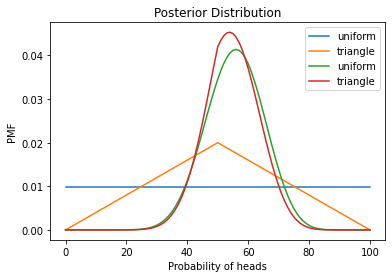
outcome = 'H'*4+'T'*1

euro1 = Pmf.from_seq(range(101), name='uniform')
euro1.plot()
euro2 = TriangularPrior()
euro2.plot()

for data in outcome:
    euro1.update(likelihood_euro, data)
    euro2.update(likelihood_euro, data)
euro1.plot()
euro2.plot()
plt.legend()
decorate_euro("Posterior Distribution")

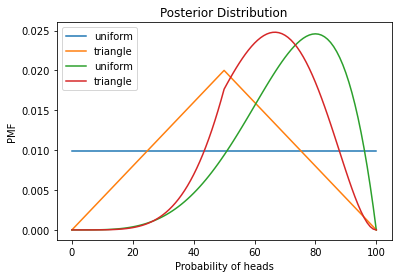
outcome = 'H'*140+'T'*110

euro1 = Pmf.from_seq(range(101), name='uniform')
euro1.plot()
euro2 = TriangularPrior()
euro2.plot()

for data in outcome:
    euro1.update(likelihood_euro, data)
    euro2.update(likelihood_euro, data)
euro1.plot()
euro2.plot()
plt.legend()
decorate_euro("Posterior Distribution")

euro1.mean() -euro2.mean()

0.20888151378589725

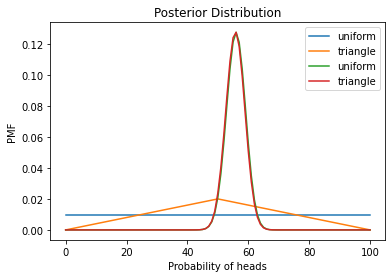
euro1.credible_interval(0.9)

array([51., 61.])

euro2.credible_interval(0.9)

array([51., 61.])

• Swammping the priors

• More or less agree for posterior

• if you start with probability zero , you will always get zero

• Avoid assigning probability to zero on everything

• Estimated proportions

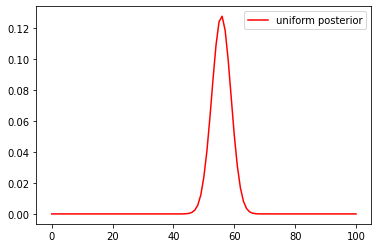
euro2.plot(color='red', label='uniform posterior')
plt.legend()

<matplotlib.legend.Legend at 0x7f98ad26e820>

list(range(51))

[0,
 1,
 2,
 3,
 4,
 5,
 6,
 7,
 8,
 9,
 10,
 11,
 12,
 13,
 14,
 15,
 16,
 17,
 18,
 19,
 20,
 21,
 22,
 23,
 24,
 25,
 26,
 27,
 28,
 29,
 30,
 31,
 32,
 33,
 34,
 35,
 36,
 37,
 38,
 39,
 40,
 41,
 42,
 43,
 44,
 45,
 46,
 47,
 48,
 49,
 50]

Interactive

def likelihood_euro(data, hypo):
#     print(data, hypo)
    x = hypo/100
    # outcome = data
    if data == 'H':
        return x
    else:
        return 1-x

def TriangularPrior(t_peak, n_range):
    """Makes a Suite with a triangular prior
    """
    
    suite = Pmf(name='triangle')
    for x in range(0, t_peak+1):
        suite[x] = x
    for x in range(t_peak+1, n_range):
        suite[x] = (n_range-1)-x
    suite.normalize()
    return suite

def compare(n_h = 140, n_t=110, t_peak=50, n_range=101):
    outcomes = 'H'*n_h+'T'*n_t

    euro1 = Pmf.from_seq(range(n_range), name='uniform')
    euro2 = TriangularPrior(t_peak, n_range)
    euro1.plot(color='steelblue', label='uniform prior', linestyle='--')
    euro2.plot(color='red', label='triangular prior', linestyle='--')

    for data in outcomes:
        euro1.update(likelihood_euro, data)
        euro2.update(likelihood_euro, data),
    euro1.plot(color='steelblue', label='uniform posterior')
    euro2.plot(color='red', label='triangular posterior')
    plt.legend()

interactive(compare, n_range=fixed(101), t_peak=fixed(50), n_h=(0,140), n_t=(0,140))