Clustering and Segmentation

Imports

import pandas as pd
import scipy as sp
import seaborn as sns
import matplotlib.pyplot as plt 
import sklearn
import numpy as np
from sklearn.preprocessing import StandardScaler
from scipy.cluster.hierarchy import dendrogram, linkage
from sklearn.pipeline import Pipeline, make_pipeline
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn import metrics
import pickle
import joblib

sns.set()

Read Dataset

df = pd.read_csv("segmentation data.csv", index_col=0); df.head()

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
ID
100000001	0	0	67	2	124670	1	2
100000002	1	1	22	1	150773	1	2
100000003	0	0	49	1	89210	0	0
100000004	0	0	45	1	171565	1	1
100000005	0	0	53	1	149031	1	1

df.columns.tolist()

['Sex',
 'Marital status',
 'Age',
 'Education',
 'Income',
 'Occupation',
 'Settlement size']

Standardization

scaler = StandardScaler()

data_norm = scaler.fit_transform(df); data_norm.shape

(2000, 7)

df_norm = pd.DataFrame(data_norm, columns = df.columns); df_norm

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
0	-0.917399	-0.993024	2.653614	1.604323	0.097524	0.296823	1.552326
1	1.090038	1.007025	-1.187132	-0.063372	0.782654	0.296823	1.552326
2	-0.917399	-0.993024	1.117316	-0.063372	-0.833202	-1.269525	-0.909730
3	-0.917399	-0.993024	0.775916	-0.063372	1.328386	0.296823	0.321298
4	-0.917399	-0.993024	1.458716	-0.063372	0.736932	0.296823	0.321298
...	...	...	...	...	...	...	...
1995	1.090038	-0.993024	0.946616	-0.063372	0.067471	-1.269525	-0.909730
1996	1.090038	1.007025	-0.760382	-0.063372	-0.084265	0.296823	-0.909730
1997	-0.917399	-0.993024	-0.418983	-1.731068	-0.906957	-1.269525	-0.909730
1998	1.090038	1.007025	-1.016432	-0.063372	-0.603329	-1.269525	-0.909730
1999	-0.917399	-0.993024	-0.931082	-1.731068	-1.378987	-1.269525	-0.909730

2000 rows × 7 columns

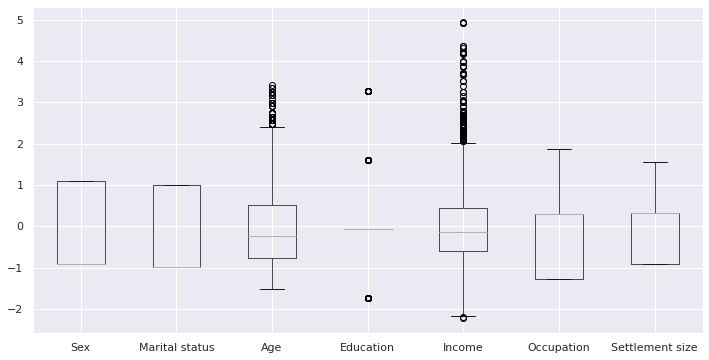
df_norm.boxplot(figsize=(12,6))#patch_artist=True, 

<AxesSubplot:>

Clustering

Hierarchial

Scipy Implementation

hier_clusters = linkage(data_norm, method='ward'); hier_clusters, hier_clusters.shape

(array([[4.78000000e+02, 1.95700000e+03, 3.41213651e-04, 2.00000000e+00],
        [6.73000000e+02, 8.21000000e+02, 3.93708059e-04, 2.00000000e+00],
        [8.67000000e+02, 9.33000000e+02, 8.92404934e-04, 2.00000000e+00],
        ...,
        [3.99200000e+03, 3.99500000e+03, 5.67337517e+01, 1.18000000e+03],
        [3.99000000e+03, 3.99400000e+03, 6.30691755e+01, 8.20000000e+02],
        [3.99600000e+03, 3.99700000e+03, 7.73495855e+01, 2.00000000e+03]]),
 (1999, 4))

plt.figure(figsize=(12,9))
plt.title("Hierarchial Clustering Dendogram")
plt.xlabel("Observations")
plt.ylabel('Distance')
dendrogram(hier_clusters, show_leaf_counts=True, no_labels=True, color_threshold=0)
plt.show()

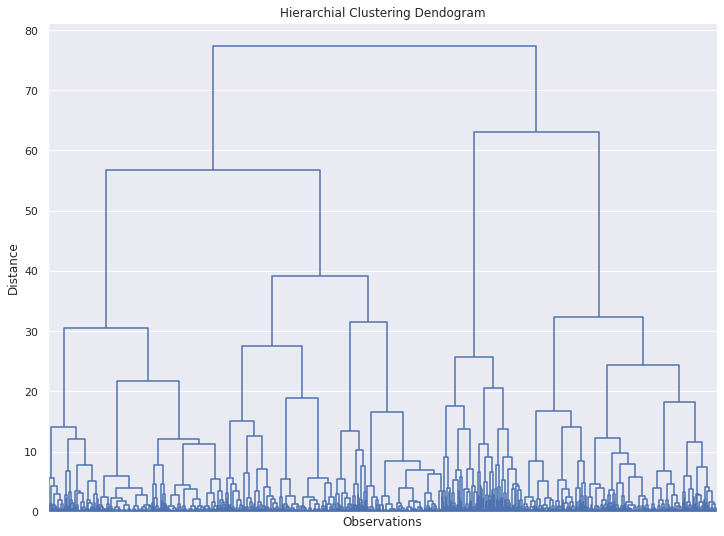
How to determine appropriate number of clusters from Hierarchial Clustering?

• Find out the largest vertical line for which there is no cutting horizontal line.

• Draw a line through the selected line and count the clusters/ group below

• Scipy dendogram algorithm already does the work for us [ Here you will draw a line on second level from top line 2]

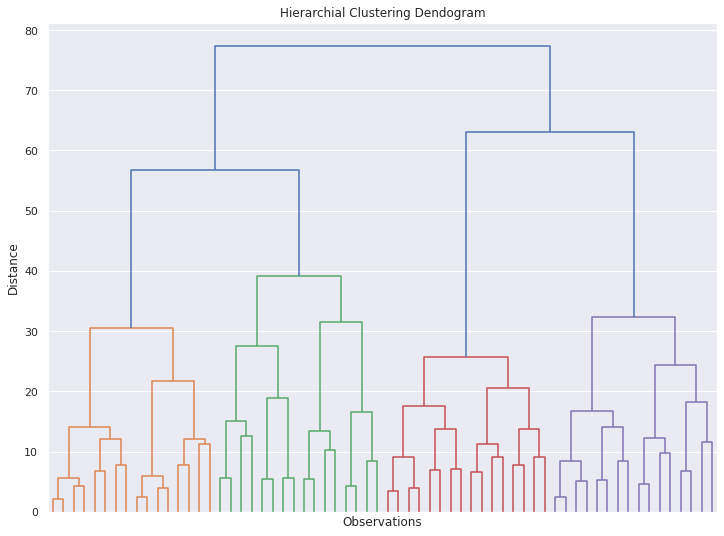
plt.figure(figsize=(12,9))
plt.title("Hierarchial Clustering Dendogram")
plt.xlabel("Observations")
plt.ylabel('Distance')
dendrogram(hier_clusters, 
           truncate_mode='level', p=5,
           show_leaf_counts=True,
           no_labels=True)
plt.show()

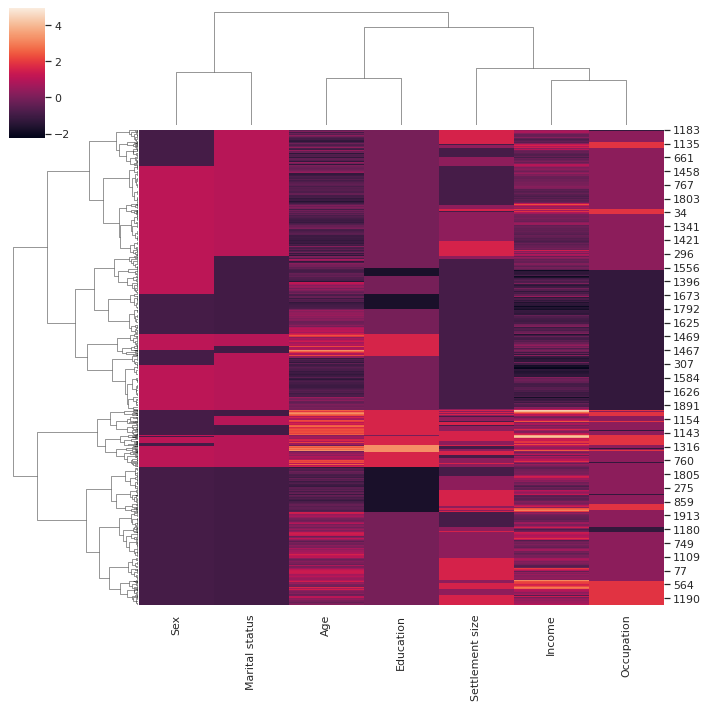
Seaborn Clustermap

sns.clustermap(df_norm, method='ward')

/opt/anaconda/envs/aiking/lib/python3.9/site-packages/seaborn/matrix.py:654: UserWarning: Clustering large matrix with scipy. Installing `fastcluster` may give better performance.
  warnings.warn(msg)

<seaborn.matrix.ClusterGrid at 0x622428ec2e0>

Kmeans

Clustering

sc = StandardScaler()
pca = PCA(n_components=4)
model = KMeans(n_clusters=4, random_state=42)
pipeline = make_pipeline(sc, pca, model); pipeline
for step in pipeline.named_steps:
    print(step)

standardscaler
pca
kmeans

m = pipeline.named_steps['pca']
m.n_components

comp_names = [f"PCA{i+1}" for i in range(m.n_components)]
comp_names

['PCA1', 'PCA2', 'PCA3', 'PCA4']

def do_clustering(df, drop_cols, pipeline):
    df_new = df.copy()
    if drop_cols: df_new = df_new.drop(columns=drop_cols, axis=1)
    y = pipeline.fit_predict(df_new)
    if 'pca' in pipeline.named_steps:
        m = pipeline.named_steps['pca']
        comp_names = [f"PCA{i+1}" for i in range(m.n_components)]
        transform_df = df_new.copy()
        for step in pipeline.named_steps:
            transform_df = pipeline.named_steps[step].transform(transform_df)
            if step == "pca": break
        pca_df = pd.DataFrame(transform_df, 
                              columns=comp_names, 
                              index=df_new.index)
        df_new = pd.concat([df_new, pca_df], axis=1)
    df_new['y'] = y+1
    return df_new, pipeline
    

df_model, trained_pipeline = do_clustering(df, drop_cols=None, pipeline=pipeline)

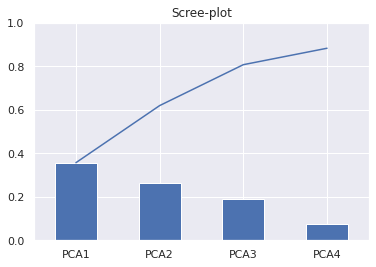
Scree plot & Visualization

m = trained_pipeline['pca']
comp_names = [f"PCA{i+1}" for i in range(m.n_components)]
df_variance = pd.DataFrame(m.explained_variance_ratio_, index=comp_names); 
ax = df_variance.plot(kind='bar', legend=False, title='Scree-plot', ylim=(0,1))
df_variance.cumsum().plot(ax=ax, legend=False)

<AxesSubplot:title={'center':'Scree-plot'}>

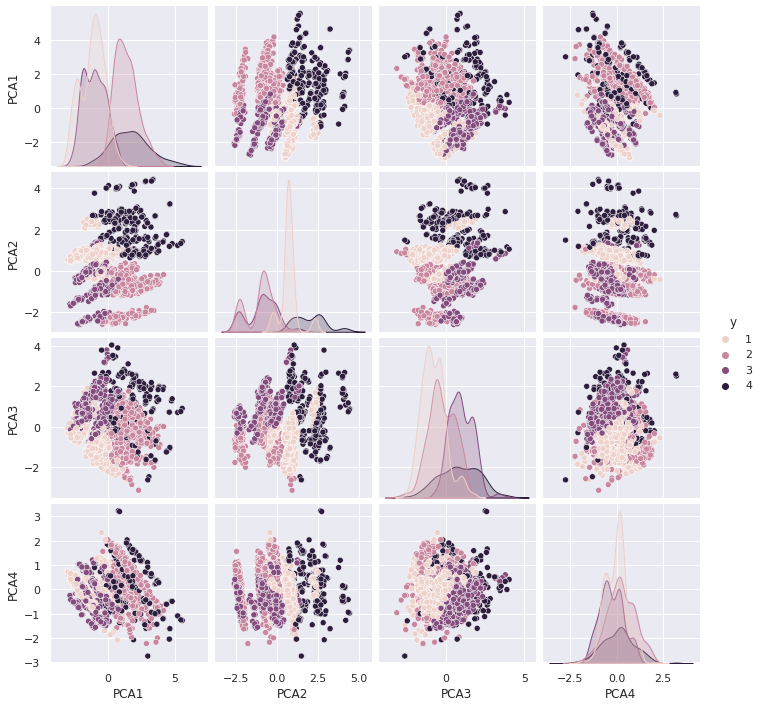
# df_model.plot.scatter(x='PCA1', y='PCA2', c='y', cmap='RdBu')

plotter_features = comp_names.copy()
plotter_features.append('y')
sns.pairplot(data=df_model[plotter_features], hue='y')

<seaborn.axisgrid.PairGrid at 0x6223d001070>

Scoring

def pipeline_callback(n_clusters):
    sc = StandardScaler()
    pca = PCA(n_components=4)
    model = KMeans(n_clusters=n_clusters, init='k-means++', random_state=42)
    pipeline = Pipeline([("sc", sc),("pca", pca), ("model", model)])
    return pipeline

def score(n_clusters,clbck, df, drop_cols=None):
    pipeline = clbck(n_clusters)
    df_new = df.copy()
    if drop_cols: df_new = df_new.drop(columns=drop_cols, axis=1)
    y = pipeline.fit_predict(df_new)
    model = pipeline['model']
    SSE = model.inertia_
    Silhouette = metrics.silhouette_score(df, y)
    CHS = metrics.calinski_harabasz_score(df, y)
    DBS = metrics.davies_bouldin_score(df, y)
    return {'SSE':SSE, 
            'Silhouette': Silhouette, 
            'Calinski_Harabasz': CHS, 
            'Davies_Bouldin':DBS, 
            'model':model}

# pipeline_callback(n_clusters=5)
score(n_clusters=5, clbck=pipeline_callback, df=df)

{'SSE': 4844.605934763394,
 'Silhouette': -0.08788670871723951,
 'Calinski_Harabasz': 364.195348701542,
 'Davies_Bouldin': 2.7414278478537,
 'model': KMeans(n_clusters=5, random_state=42)}

df_cluster_scorer = pd.DataFrame()
df_cluster_scorer['n_clusters'] = list(range(2, 11))
df_cluster_scorer

	n_clusters
0	2
1	3
2	4
3	5
4	6
5	7
6	8
7	9
8	10

df_cluster_scorer['SSE'],df_cluster_scorer['Silhouette'],\
df_cluster_scorer['Calinski_Harabasz'], df_cluster_scorer['Davies_Bouldin'],\
df_cluster_scorer['model'] = zip(*df_cluster_scorer['n_clusters'].map(lambda row: score(row,
                                                                                        pipeline_callback, 
                                                                                        df, 
                                                                                        drop_cols=None).values()))
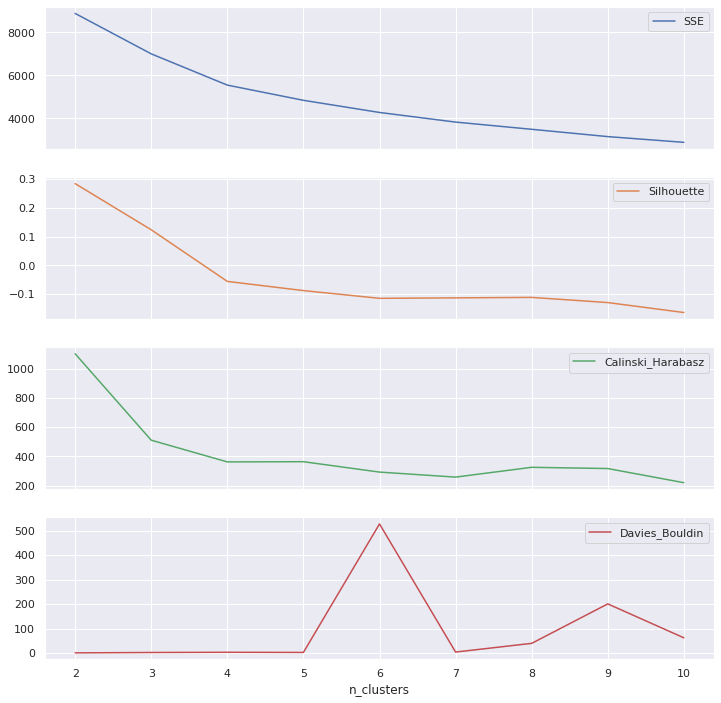
df_cluster_scorer

	n_clusters	SSE	Silhouette	Calinski_Harabasz	Davies_Bouldin	model
0	2	8880.414629	0.283954	1102.121434	1.020794	KMeans(n_clusters=2, random_state=42)
1	3	7002.392373	0.123472	511.298912	2.516972	KMeans(n_clusters=3, random_state=42)
2	4	5550.669973	-0.055975	362.742657	3.339190	KMeans(n_clusters=4, random_state=42)
3	5	4844.605935	-0.087887	364.195349	2.741428	KMeans(n_clusters=5, random_state=42)
4	6	4280.231528	-0.114802	293.145249	528.028205	KMeans(n_clusters=6, random_state=42)
5	7	3832.921508	-0.113219	258.881753	4.254454	KMeans(n_clusters=7, random_state=42)
6	8	3498.065117	-0.111513	325.874041	39.848429	KMeans(random_state=42)
7	9	3158.496071	-0.129571	317.344098	201.169169	KMeans(n_clusters=9, random_state=42)
8	10	2892.091797	-0.164104	220.717341	62.522815	KMeans(n_clusters=10, random_state=42)

df_cluster_scorer.plot.line(subplots=True,x ='n_clusters', figsize=(12,12))

array([<AxesSubplot:xlabel='n_clusters'>,
       <AxesSubplot:xlabel='n_clusters'>,
       <AxesSubplot:xlabel='n_clusters'>,
       <AxesSubplot:xlabel='n_clusters'>], dtype=object)

Results

PCA Component Intuition

m = trained_pipeline['pca']
pca_loadings = pd.DataFrame(m.components_, columns=df.columns, index = comp_names); pca_loadings

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size
PCA1	-0.314695	-0.191704	0.326100	0.156841	0.524525	0.492059	0.464789
PCA2	0.458006	0.512635	0.312208	0.639807	0.124683	0.014658	-0.069632
PCA3	-0.293013	-0.441977	0.609544	0.275605	-0.165662	-0.395505	-0.295685
PCA4	-0.315601	0.280454	-0.009506	0.181476	-0.482600	-0.281690	0.690265

figure, axes = plt.subplots(1, 3, sharex=True, sharey=True, figsize=(21,4))
figure.suptitle('PCA Loadings')

sns.heatmap(pca_loadings, 
            cmap='RdBu', 
            annot=True, 
            vmin=-1, 
            vmax=1, ax=axes[0]).set(title="Loading Correlation")
sns.heatmap(np.abs(pca_loadings), 
            cmap='Greens', 
            annot=True, ax=axes[1]).set(title="Loading Importance")
sns.heatmap(np.abs(pca_loadings)>np.abs(pca_loadings).mean().mean(), 
            cmap='Greens', 
            annot=True, ax=axes[2]).set(title=f"Loading Importance cutoff={np.abs(pca_loadings).mean().mean()}")

[Text(0.5, 1.0, 'Loading Importance cutoff=0.33289014252885146')]

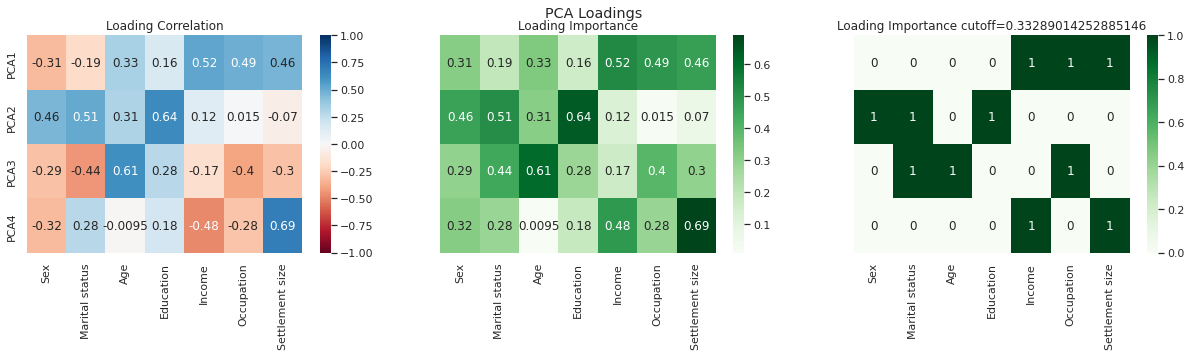
• PCA1: Carrier Focussed

• PCA2: Education & Lifestyle

• PCA3: Experience

Cluster Analysis

df_analysis = df_model.groupby(['y']).mean(); df_analysis

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	PCA1	PCA2	PCA3	PCA4
y
1	0.905045	0.986647	28.873887	1.063798	107576.228487	0.672107	0.439169	-1.122432	0.733291	-0.797918	-0.019662
2	0.026178	0.178010	35.624782	0.734729	140950.319372	1.267016	1.520070	1.381089	-1.044848	-0.273292	0.211736
3	0.319018	0.089980	35.259714	0.768916	95850.155419	0.296524	0.038855	-0.987777	-0.882022	0.965476	-0.271684
4	0.503788	0.689394	55.689394	2.128788	158209.094697	1.125000	1.106061	1.697646	2.029427	0.841953	0.093869

Segment Interpretation and Labelling

• 1 : More Female mostly married , youngest group avg education, tending towards small areas and cities – Standard (May be female)

• 2 : Next Highest income, mostly male Age 35 avg, Education lowest Income high, occupation highest, settlement tending to cities – Career Focussed (Mostly male)

• 3 : Lowest occupation and income lower end of education –Fewer Opportunities

• 4 : Highest Income, Education, Oldest, Sex 50-50, Occupation, Settlement in between – Well Off

names = {1:"Standard",
                    2:"Career-Focussed",
                    3:"Fewer-Opportunities",
                    4:"Well-off"}
df_analysis["Segment Names"] = list(names.values())
df_analysis.set_index(["Segment Names"], inplace=True)

df_analysis

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	PCA1	PCA2	PCA3	PCA4
Segment Names
Standard	0.905045	0.986647	28.873887	1.063798	107576.228487	0.672107	0.439169	-1.122432	0.733291	-0.797918	-0.019662
Career-Focussed	0.026178	0.178010	35.624782	0.734729	140950.319372	1.267016	1.520070	1.381089	-1.044848	-0.273292	0.211736
Fewer-Opportunities	0.319018	0.089980	35.259714	0.768916	95850.155419	0.296524	0.038855	-0.987777	-0.882022	0.965476	-0.271684
Well-off	0.503788	0.689394	55.689394	2.128788	158209.094697	1.125000	1.106061	1.697646	2.029427	0.841953	0.093869

df_analysis['Segment-Size'] = df_model.groupby("y").count()[df_model.columns[0]].tolist()

df_analysis['Segment-Prop'] = df_analysis['Segment-Size']/ df_analysis['Segment-Size'].sum()

df_analysis

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	PCA1	PCA2	PCA3	PCA4	Segment-Size	Segment-Prop
Segment Names
Standard	0.905045	0.986647	28.873887	1.063798	107576.228487	0.672107	0.439169	-1.122432	0.733291	-0.797918	-0.019662	674	0.3370
Career-Focussed	0.026178	0.178010	35.624782	0.734729	140950.319372	1.267016	1.520070	1.381089	-1.044848	-0.273292	0.211736	573	0.2865
Fewer-Opportunities	0.319018	0.089980	35.259714	0.768916	95850.155419	0.296524	0.038855	-0.987777	-0.882022	0.965476	-0.271684	489	0.2445
Well-off	0.503788	0.689394	55.689394	2.128788	158209.094697	1.125000	1.106061	1.697646	2.029427	0.841953	0.093869	264	0.1320

df_model['labels'] = df_model['y'].map(names)
df_model

	Sex	Marital status	Age	Education	Income	Occupation	Settlement size	PCA1	PCA2	PCA3	PCA4	y	labels
ID
100000001	0	0	67	2	124670	1	2	2.514746	0.834122	2.174806	1.217794	4	Well-off
100000002	1	1	22	1	150773	1	2	0.344935	0.598146	-2.211603	0.548385	1	Standard
100000003	0	0	49	1	89210	0	0	-0.651063	-0.680093	2.280419	0.120675	3	Fewer-Opportunities
100000004	0	0	45	1	171565	1	1	1.714316	-0.579927	0.730731	-0.510753	2	Career-Focussed
100000005	0	0	53	1	149031	1	1	1.626745	-0.440496	1.244909	-0.231808	2	Career-Focussed
...	...	...	...	...	...	...	...	...	...	...	...	...	...
100001996	1	0	47	1	123525	0	0	-0.866034	0.298330	1.438958	-0.945916	3	Fewer-Opportunities
100001997	1	1	27	1	117744	1	0	-1.114957	0.794727	-1.079871	-0.736766	1	Standard
100001998	0	0	31	0	86400	0	0	-1.452298	-2.235937	0.896571	-0.131774	3	Fewer-Opportunities
100001999	1	1	24	1	97968	0	0	-2.241453	0.627108	-0.530456	-0.042606	1	Standard
100002000	0	0	25	0	68416	0	0	-1.866885	-2.454672	0.662622	0.100896	3	Fewer-Opportunities

2000 rows × 13 columns

names

{1: 'Standard', 2: 'Career-Focussed', 3: 'Fewer-Opportunities', 4: 'Well-off'}

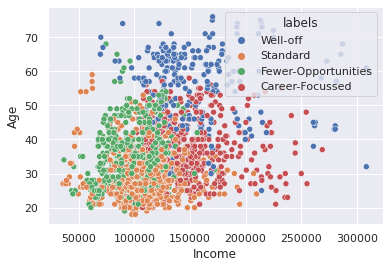
sns.scatterplot(data=df_model, x='Income', y='Age',hue='labels')

<AxesSubplot:xlabel='Income', ylabel='Age'>

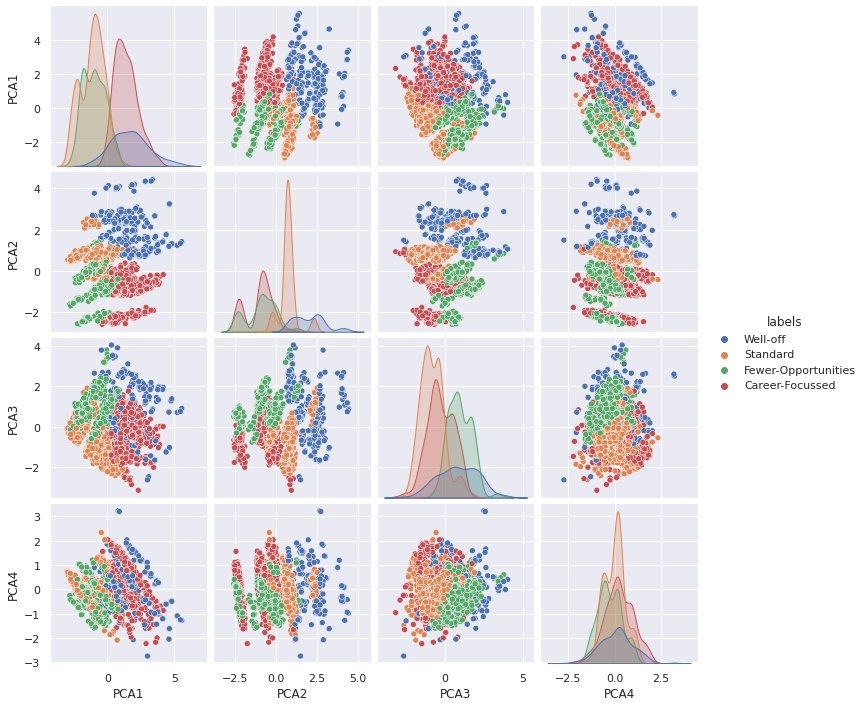
plotter_features = comp_names.copy()
plotter_features.append('labels')
sns.pairplot(data=df_model[plotter_features], hue='labels')

<seaborn.axisgrid.PairGrid at 0x62236c36760>

Export

# trained_pipeline.export("cluster_pipeline.pickle")
joblib.dump(trained_pipeline, "cluster_pipeline.pkl")

['cluster_pipeline.pkl']

print("Enfin")

Enfin